Hypercubed

In early Dec. 1999 I purchased the hypercubed.net domain name (followed shortly by hypercubed.com in April 2000). While working on the look an feel of the hypercubed website I wanted to create some 3D projections of hypercubes  to decorate the front page. But I didn't want a simple picture of a hypercube.  I wanted it to rotate four dimensionally. I could have just created a few images of a hypercube by hand and combined them into an animated gif but my graphics skills were (are) very poor.  Plus it wouldn't have been very cool. So I decided to create a POV-RAY script to create hypercubes for me. The script I made didn't simply draw a hypercube but was actually a set of macros that allowed me to define and view projections of any four dimensional object in which the 4 dimensional coordinates of the object's vertices are known.  Using the macros I was able to create the hypercube animated gifs that still adorn the hypercubed.com website today.  In March 2000 (6 years now) I wrote a how-to article documenting my POV-RAY macros for visualizing four dimension objects.  This page has been sitting on the hypercubed.com, relativity unnoticed, ever since.  So here for your retro viewing pleasure is the original text of that article.

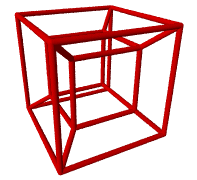You may be wondering, "What is a Hypercube?" A Hypercube is a four (4) dimensional equivalent of a cube. A line is a one (1) dimensional object. Now imagine if you were to make a duplicate of this line and then connect these two lines by more lines of the same length. This would be a two (2) dimensional square. Now take this square and connect it to a duplicate square using more squares of the same size. You now have two squares connected by four squares, six faces in all. This is a three (3) dimensional cube. Now the hard part; imagine two cubes where each face of one cube is connected to the other cube by duplicate cubes. This is difficult to imagine because we think in three dimensions. But mathematically there is no difference between space with three dimensions and space with four dimensions.

So what does a hypercube look like? Well obviously, due to limitations of 3-d space, we cannot see a four dimensional object. However, using the same techniques that one uses when drawing a 3 dimensional cube onto a two dimensional piece of paper we can project an image of a four dimensional hypercube (or the wire frame of one) into three dimensions.

POV-RAY is a 3-d is a ray tracer. It takes simple text file descriptions of a three dimensional scene and renders it into a graphics scene. So here is the challenge. Given a set of 4 vectors (four dimensional vectors) that represent a four dimensional object (such as a hypercube) how can these be projected into a 3-d scene.

Before we can work with 4 vectors we must first "teach" POV-RAY how to manipulate 4 vectors.

 #macro v4dot (A, B)  //4d dot product
       A.x*B.x+A.y*B.y+A.z*B.z+A.t*B.t
 #end

#macro v4len(V)  //Length of 4 vector
     sqrt(v4dot(V, V))
 #end
 
 #macro Norm4(V)  //Normalize 4 vector
     V/v4len(V)
 #end
 
#macro Cross4 (U, V, W)  // 4d cross product

    // Calculate intermediate values.

    #local A = (V.x * W.y) - (V.y * W.x);
    #local B = (V.x * W.z) - (V.z * W.x);
    #local C = (V.x * W.t) - (V.t * W.x);
    #local D = (V.y * W.z) - (V.z * W.y);
    #local E = (V.y * W.t) - (V.t * W.y);
    #local F = (V.z * W.t) - (V.t * W.z);

    // Calculate the vector components.

    #local X = ((U.y * F) - (U.z * E) + (U.t * D));
    #local Y = ((U.x * F) + (U.z * C) - (U.t * B));
    #local Z = ((U.x * E) - (U.y * C) + (U.t * A));
    #local T = (-(U.x * D) + (U.y * B) - (U.z * A));
    
    <X, Y, Z, T>
#end

The next step is to translate the 4 dimensional vectors into the 3 dimensional eye coordinates using a transformation matrix.

#macro v4to3 (A)
        #local V = v4dotM(A-From4, TM);  //Translate to eye coordinates
        #if (Per4 = 1)
                #local R = (V.t*Tp);  //4d Perspective
        #else
                #local R = v4len(From4); //4d Orthogonal
        #end        
        <V.x/R,V.y/R,V.z/R>  //3d vector
 #end

TM (the transformation matrix) is a 4x4 matrix calculated using the eye coordinates.

#declare Tp = tan((2*pi/360)*45);

#declare From4 = <4, 0, 0, 0>;
#declare To4 = <0, 0, 0, 0>;
#declare Up4    = <0, 1, 0, 0>; 
#declare Over4  = <0, 0, 1, 0>; 
#declare Per4 = 1;  //1- Perspective 0- Orthogonal

#declare D = Norm4(To4 - From4);
#declare A = Norm4(Cross4(Up4, Over4, D));
#declare B = Norm4(Cross4(Over4, D, A));
#declare C = Cross4(D, A, B);

#declare TM =   //Translation Matrix
array[4]
{ A, B, C, D }

To "rotate" the object, simply rotate the From4 vector. For example:

#declare T = pi/2*clock;
#declare From4 = 4*<cos(T), 0, -sin(T), 0>;

Now we must describe what to draw. I have defined two basic "objects". A point and a vector.

#macro point3d (P, pradius, pcolor)
 sphere
 {
  P
  pradius
  pigment { pcolor }
 }
 #end
  
 #macro point4d (P, pradius, pcolor)
        point3d (v4to3(P), pradius, pcolor)
 #end 
 
 #macro vector3d (S, E, vradius, vcolor)
 #if (!((S.x = E.x) & (S.y = E.y) & (S.z = E.z)))
 cone
 {
  S, vradius,
  E, vradius
  pigment { vcolor }
 }
 #end 
 #end
 
#macro vector4d (S, E, vradius, vcolor)
 vector3d (v4to3(S), v4to3(E), segradius, vcolor)
#end

The 'point4d' macro will place a point in 4-space and 'vector4d' will draw a cylinder from one 4-space point to another. With these two functions/macros one can render 4-d wire frame projections in POV-RAY as long as they know the 4 dimensional coordinates of the object they are describing. For the case of a Hypercube the 4-d coordinates are <±1, ±1, ±1, ±1>.

Hypercube.pov v1.0 4.57 kb

Special thanks to Steven Richard Hollasch and his Thesis on Four-Space Visualization of 4D Objects (August 1991)